Submitted by jonas on
De stelling van Taylor handelt over afleidbare functies. De eenvoudigste afleidbare functies zijn veeltermen, dit zijn functies van de vorm $f(x) = a_0 + a_1x + a_2x^2 + \ldots + a_nx^n$ met $n$ een natuurlijk getal en $a_0, a_1, \ldots, a_n \in \mathbb{R}$. De stelling van Taylor zegt nu dat elke andere afleidbare functie rond een punt willekeurig dicht benaderd kan worden door een veelterm. Men kan dus een veelterm opstellen die in de buurt van een bepaald punt bijna gelijk is aan de oorspronkelijke functie. Deze wordt de Taylorbenadering genoemd. Voor de kenners wordt de formule gegeven door
$$f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \ldots + \frac{f^{(n)}(a)}{n!}(x-a)^n + \ldots.$$ Wanneer de ontwikkeling oneindig ver wordt doorgevoerd, spreekt men van de Taylorreeksontwikkeling of kortweg de Taylorreeks.
Wat is een goede manier om te meten hoe belangrijk een stelling is? Er zijn in elk geval twee criteria die zeer goede maatstaven vormen. Ten eerste kan men kijken in hoeveel domeinen de stelling relevant is en ten tweede hoe vaak ze dan effectief toegepast wordt. De stelling van Taylor doorstaat beide testen met verve. Sterker nog, haar brutale efficiëntie is zo into your face dat ze nauwelijks geëvenaard wordt. De Taylorbenadering duikt zo vaak op dat men bijna zou gaan vergeten dat dit wel degelijk een echte stelling is en niet één of andere definitie of axioma in verband met afleidbaarheid. Zo alomtegenwoordig is de stelling van Taylor dat reusachtige domeinen van de wiskunde ondenkbaar zouden zijn zonder het bestaan van deze stelling. Vooral de numerieke wiskunde en de ganse theoretische fysica zouden het maar pover stellen indien ze hun functies niet konden benaderen door veeltermen.
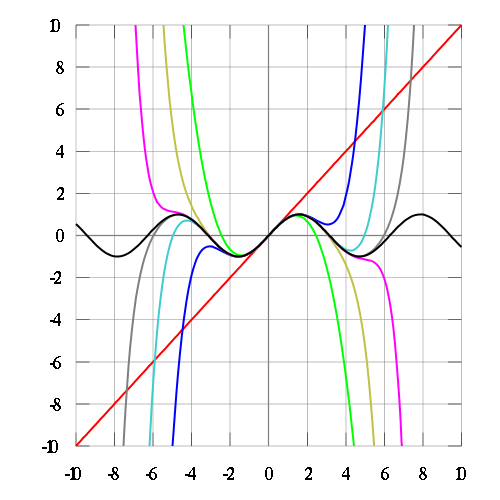
Opeenvolgende taylorbenaderingen van $\sin(x)$ rond het punt $0$ van graad $1$ (rood),
$3$ (groen), $5$ (blauw), $7$ (bruin), $9$ (appelblauwzeegroen), $11$ (paars) en $13$ (grijs).
Maar waarom wordt deze stelling eigenlijk zo vaak gebruikt, wat maakt ze zo nuttig? Er zijn immers nog andere benaderingsstellingen, de bekendste waarschijnlijk de Fourierreeks, maar die duiken toch net iets minder op of worden enkel in specifiekere contexten gebruikt. De reden is de gedaante van de benaderende functie. Dit is een veelterm, en veeltermen zijn bijzonder dankbare functies om mee te werken. Dit laat zich op zeer vele vlakken voelen.
Vele problemen rond functies zijn zeer lastig voor algemene afleidbare functies, maar zeer eenvoudig voor veeltermen. Integratie, asymptotisch gedrag en differentiaalvergelijkingen zijn maar enkele voorbeelden. Telkens opnieuw zal men de bestudeerde functies vervangen door hun Taylorbenaderingen die de oplossing van het probleem sterk vergemakkelijken. Daarna kan men de Taylorbenadering opnieuw vervangen door de bijhorende functie en zo de oplossing reconstrueren. Of, zoals in de numerieke wiskunde en de fysica, zal men functies vervangen door een Taylorbenadering van een bepaalde orde en dan benaderend verderwerken. Het woord 'linearisatie' duikt hier onvoorstelbaar vaak op en dit komt neer op het toepassen van de stelling van Taylor voor $n = 1$.
De stelling van Taylor spreekt misschien niet zo tot de verbeelding als andere stellingen, noch heeft ze een rijke geschiedenis. Maar toen de Brit Brook Taylor ze in 1712 opstelde, wist deze man zeer goed waar hij mee bezig was. De volledigheid gebiedt ons hier op te merken dat de Schotse wiskundige James Gregory al vroeger Taylorreeksen opstelde voor verscheidene goniometrische functies. Taylor bewees de algemene stelling. En daarmee gaf hij de wiskunde een nieuw instrument, en dit instrument zou zich geruisloos ontpoppen tot één van de meest gebruikte binnen de ganse wiskunde. Dit is geen stelling die zichzelf opdringt aan de mensen, die zich sexy kleedt en bij allen rondom zich erotische fantasieën teweegbrengt. Neen, de stelling van Taylor is niet de door paparazzi gestalkte beroemdheid. Deze stelling verkiest een rustig leven op het platteland, weg van de drukte. Laat ons echter niet de fout maken om ze dan ook af te schrijven als onbelangrijk. Neen, de stelling van Taylor zou veel harder gemist worden dan zijn naar de spotlichten verlangende tegenhangers. Achteraf zou iedereen beseffen dat ze een valse profeet aan het aanbidden waren, en dat de echte zich al die tijd achter de schermen had bevonden.
