Stel je hebt een piramide van getallen, zoals die hieronder. Een padsom is de som van alle getallen die je tegenkomt als je, vanuit de top vertrekkend, telkens afdaalt naar één van de twee vakjes eronder. Hoe zou je (algemeen) de maximale padsom naar de onderste rij vinden? Bijvoorbeeld voor de piramide hieronder is de maximale som 23: er bestaat een pad met padsom 3 + 7 + 4 + 9 = 23, en er bestaat geen zo'n pad met grotere padsom.
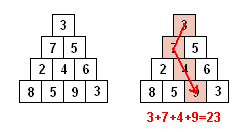
Een mogelijke manier om dit te bepalen is om gewoon alle paden uit te proberen, in ons voorbeeld moet je dan 2^3=8 paden uitproberen (drie keer kiezen tussen naar links of naar rechts).

Voor een piramide van hoogte 100 moet je dan echter al 2^99 paden afgaan, wat zelfs op de snelste computers nog biljoenen jaren zou duren.
Maar je kunt ook slim gebruik maken van volgende observatie: in elk vakje hangt de maximale padsom er naar toe enkel af van de maximale padsommen naar elk van de twee vakjes erboven. Als je dus rij per rij (vanaf rij 2) alle vakjes overschrijft door zichzelf plus het maximum van de twee vakjes erboven, dan heb je op het einde onderaan de maximale padsom naar elk van de vakjes onderaan. Het maximum van de nieuwe onderste rij is dus de gezochte maximale padsom.

Dit gaat veel sneller: bij een piramide van hoogte 100 vraagt dit dus slechts 2+3+...+99=4949 rekenstappen, plus het zoeken van een maximum van 100 getallen, wat een moderne computer in minder dan een seconde kan. Het programmeerwerk is zelfs heel eenvoudig: stockeren we de elementen van de piramide in een benedendriehoeksmatrix, dan geeft volgend Maple-scriptje meteen het resultaat.
n:=4; A:=Matrix(n,n,[[3,0,0,0],[7,5,0,0],[2,4,6,0],[8,5,9,3]]);
for i from 2 to n do
A[i,1]:=A[i,1]+A[i-1,1];
for j from 2 to i do
A[i,j]:=A[i,j]+max(A[i-1,j-1],A[i-1,j]);
end do:
end do:
A; maximum = max(seq(A[n,i],i=1..n));
Probeer gerust eens uit op je favoriete 100x100 piramide, het zou een ideale coma-vraag zijn!
