Submitted by jonas on
De centrale limietstelling is een stelling uit de statistiek. Zeer bekend is de normale verdeling. Haar grafiek wordt ook wel de klok van Gauss genoemd. Wanneer men nu een random steekproef neemt van onafhankelijke variabelen met dezelfde verdeling, dan zegt de centrale limietstelling dat het gemiddelde van deze steekproef bij benadering normaal verdeeld zal zijn. Dus als men steeds opnieuw een steekproef neemt met dezelfde grootte, en telkens het gemiddelde optekent, bekomt men bij benadering de grafiek van een normale verdeling. Hoe groter de steekproef, hoe beter de benadering. Het steekproefgemiddelde is dus normaal verdeeld, onafhankelijk van de onderliggende verdeling van de grootheid waarvan men een steekproef neemt.
Dit wordt geillustreerd op de figuur. De steekproef bestaat hier uit het aantal keer kop bij het honderdmaal opwerpen van een munt. Dus men werpt een munt honderd keer en noteert het aantal kop, en herhaalt dit procédé een groot aantal keer. Dan wordt de bijgevoegde grafiek bekomen.
De statistiek is zonder twijfel de bekendste en meest verspreide tak van de wiskunde. Zeer veel diploma's, die vaak helemaal niets met wiskunde te maken hebben, veronderstellen toch een zekere kennis van statistiek. Elke krant staat dagelijks vol met statistische uitspraken. Overal wordt statistiek toegepast, in de economie, de geneeskunde, de psychologie en natuurlijk ook in de exacte wetenschappen zelf zoals biologie, chemie, fysica enzovoort. Wetenschappelijk onderzoek zonder statistiek is volledig ondenkbaar.
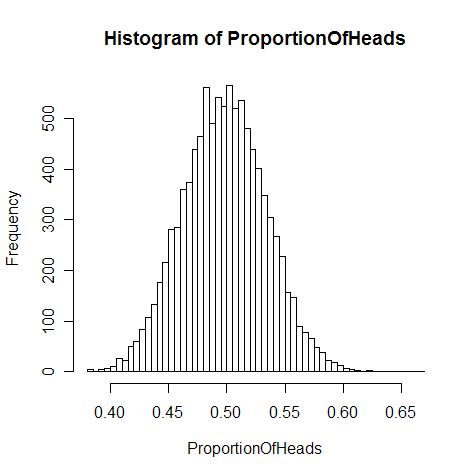
De centrale limietstelling in actie bij het werpen van een munt.
De centrale limietstelling is, samen met de wet van de grote aantallen, de fundamentele stelling van de statistiek. In tegenstelling tot de wet van de grote aantallen ligt ze echter niet echt voor de hand, en het is dan ook een resultaat dat menige statisticus wel eens een dankbare blik naar de hemel doet werpen. Een wereld zonder centrale limietstelling zou een vreselijke wereld zijn, een helse bol van verderf. Het is volkomen onmogelijk om de pracht van de centrale limietstelling met teveel lof te overzaaien. Het is een stelling die, wanneer ze door een jonge wiskundige voor het eerst aanschouwd wordt, hem in tranen doet uitbarsten en hem opnieuw doet beseffen waarom hij voor deze wetenschap gekozen heeft. Het is een kunstwerk, een delicaat juweel, met zorg en precisie gesmeed, intens prachtig met een verlokkelijke schittering die iedereen in de ban houdt.
De statistiek wordt vanzelfsprekend het meest gebruikt om hypothesen te testen. De termen nulhypothese, p-waarde en steekproefgemiddelde zullen weinig wetenschappers onbekend in de oren klinken. De centrale limietstelling nu is de stelling die dit allemaal mogelijk maakt. Zij zorgt voor een pad in het duistere bos der kansverdelingen. Bij het afnemen van een steekproef is zelden de onderliggende verdeling gekend, en toch kan men uitspraken doen over de gemiddelde waarde. Dit is volledig te danken aan de centrale limietstelling, die dit gemiddelde een regel oplegt los van de onderliggende kansverdeling. De centrale limietstelling houdt het steekproefgemiddelde in bedwang, sluit het op in de Gaussische kooi waaruit het nooit kan ontsnappen. Dit, en alleen dit, laat wetenschappers toe het nauwkeurig te bestuderen, te observeren en stelt hen in staat te concluderen.
Want, mocht de verdeling van het steekproefgemiddelde afhankelijk zijn van de onderliggende verdeling, een resultaat dat men intuïtief tot op zekere hoogte zelfs zou verwachten, zou het onmogelijk zijn om concrete uitspraken te doen over vele wetenschappelijke resultaten. In de theoretische statistiek duiken vrijwel constant limieten van steekproefgemiddeldes op, en deze kunnen dankzij de centrale limietstelling zonder verpinken vervangen worden door een normale verdeling. Zou dit niet mogelijk zijn, dan zou de ganse theorie rond het schatten van parameters in elkaar storten wat dan weer rampzalig zou zijn voor de praktijk. Onderzoeken vergelijken zou herleid worden tot een quasi onmogelijke opgave, en de statistiek in het algemeen zou veel, veel, veel lastiger en ingewikkelder worden.
